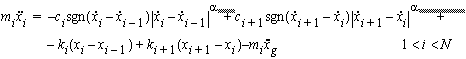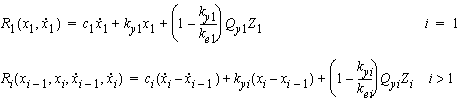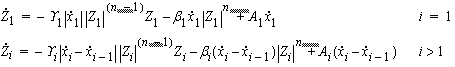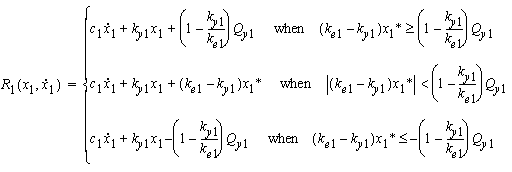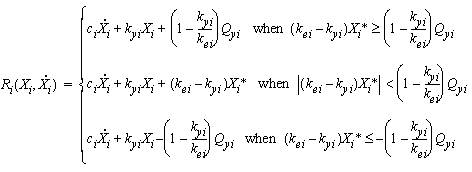Help Page for the Java-Powered Simulation for Nonlinear Multi-Story Buildings

---

Table of Contents Introduction How to Use the Simulation Technical Background Homework References
	Page created by Yong Gao, 01/08/2004
Go to the Java-Powered Simulation for Nonlinear Multi-Story Buildings

---

Introduction

Welcome to the help page of the Java-Powered Simulation for Nonlinear Multi-Story Buildings.

It is common to design structures to behave nonlinearly under extreme load conditions, e.g. earthquakes and hurricanes. Therefore, it is important to instruct students or practitioners to better understand the effect of nonlinear behavior of buildings.  This nonlinear dynamic analysis virtual laboratory (VL) has been developed for his purpose.

In this VL, users are given wide flexibility to perform dynamic analysis. Users can choose the number of stories, as well as select the floor mass, stiffness, and damping coefficients for each story. Four models, are provided to portray the behavior of the structure. These modes are: (a) linear stiffness and linear viscous damping; (b) linear stiffness and nonlinear power-law damping; (c) hysteretic stiffness using the Bouc-Wen model and linear viscous damping; and (d) hysteretic bilinear stiffness and linear viscous damping. The same type of model is employed for all columns, but the parameters defining this model can be varied for each story. Sinusoidal and four historical earthquake excitations can be chosen for conducting the dynamic analysis.

This document offers a description of how to operate and use the Java-Powered Simulation for Nonlinear Multi-Story Building, a picture of which is shown below, and also the technical background of this simulation. A number of "homework" problems (or exercises) are suggested and references are provided.

Response Frame	Response Frame	Control Panel
Response Frame	Response Frame

 

Figure 1. Java-Powered Simulation Applet

How to Use the Simulation

 

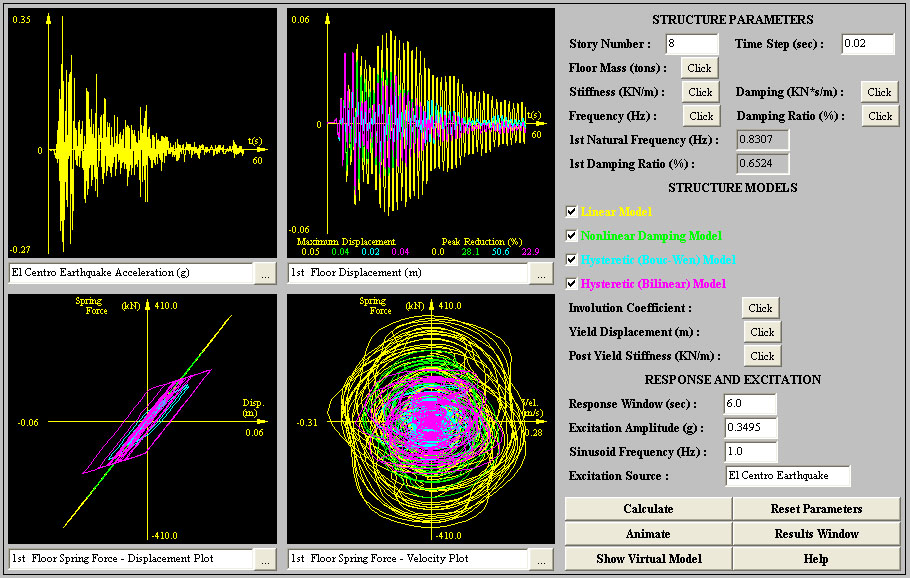
As shown in Figure 1, there are four response frames on the left of the user interface. On the right, there is a control panel for conducting structural analysis and changing parameters. There is also an animation panel which provides the animated response through a virtual building model. This panel is shown in Figure 2. The control panel and animation panel are interchanged with each other by clicking the “Show Virtual Model” or “Show Control Panel” button located at the lower corner of their panels. A description of each of these components is given below. Control Panel Located on the far right of the simulator, this panel is used to enter specific data for the structure and excitation. This panel also contains buttons to do calculation and animation and the button which links to this help page. Structure Parameters Story Number: total number of stories. The default is 8 stories. Time Step: time step for numerical computation. A default time step has been preset as 0.02 seconds. A smaller time step is expected when the structure is getting stiffer. Floor Mass: a dialogue box (Figure 3) will open when the selection button is pushed, which allows users to input floor mass for each floor. The default value is 8.0 tons. Stiffness: linear stiffness for each story. The default value is 7000 KN/m. Damping: viscous damping coefficient for each story. The default value is 10.0 KN*s/m. Frequency: natural frequencies associated with the structural parameters. These natural frequencies are automatically updated when any structural parameters are changed. Damping Ratio: damping ratio associated with the structural parameters. These damping ratios are automatically updated when any structural parameters are changed. 1st Natural Frequency: for convenience, the first natural frequency is displayed in the main interface. 1st damping Ratio: for convenience, the first damping ratio is displayed in the main interface.         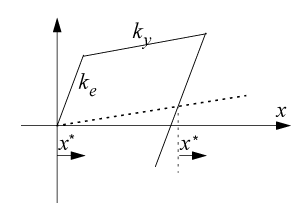Structure Models Structure Models: by checking one or more of the following checkboxes, desired
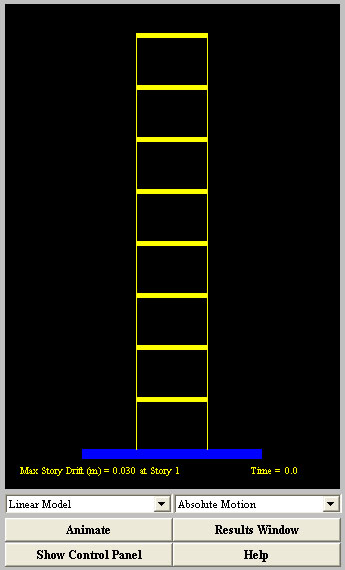
	Figure 2. Animation Panel
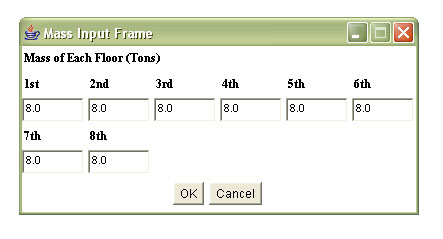
	Figure 3. Mass Input Frame

        analysis results can be displayed. The default is to display the structural behavior

        described by linear model.

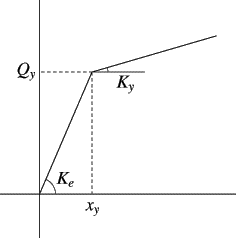
Involution Coefficient: parameters associated with the nonlinear damping model. The default is 0.5. Yield Displacement: displacement when exceeded, the Bouc-Wen model and the bilinear model change from elastic to plastic region. The default is 0.02 m. Response Window: width of the response frames (in seconds) during the animation. The default is 6.0 seconds.         Response and Excitation Excitation Amplitude: by changing this value, the excitation magnitude can be scaled. Sinusoid Frequency: frequency component for the sinusoid excitation. The default value is 1.0 Hz. Excitation Source: display the name of the current excitation. The default excitation is the El Centro Earthquake.         Action Buttons Calculate: conduct calculation. Reset Parameters: resets all the parameters to default values. Animate: start/stop animation in the response frames as well as the animation panel. Results Window: display important analysis results after each computation. Show Virtual Model: by clicking this button, the control panel and animation panel are interchanged with each other. Help: pop up the help page when pushed. Animation Panel The animation frame, interchangeable with the control panel, shows the behavior of the multi-story building under the specified excitation. Buildings, described using Linear Model, Nonlinear Damping Model, Bouc-Wen Model and Bilinear Model, can be animated by the appropriate selection in the left choice of this frame. The user can also choose to animate absolute or relative motion of the structure: Absolute Motion: Display the absolute motion of the structure. Thus, the ground is seen moving. Relative Motion: Display the motion of the structure relative to the ground. Thus, the ground is seen not moving.

Response Frames

There are four response frames on the left of the simulator. The functions of these four response frames are identical, except that the top left frame can also display the earthquake excitation. There is a selection button at the lower right corner of each frame. For the top left frame, this selection button brings up a dialogue box (shown in Figure 4) for user to select the earthquake excitation or response to display. For the other three response frames, the selection button brings up a similar dialogue box for a response selection only. Peak response information such as the maximum value of each response, peak reduction (= maximum peak of each case / maximum peak of Linear Model case * 100 (%)) is displayed in the bottom of this frame. On the top left of the simulator, the response frame can show current excitation signal, either in displacement or acceleration. Five historical excitation records are available for simulation: Sinusoidal Input: the default value of the frequency is 1.0 Hz. The default value of the maximum acceleration is 0.3g. El Centro Earthquake: North-south component recorded at the Imperial Valley Irrigation District substation in El Centro, California, during the Imperial Valley, California earthquake of May 18, 1940. The magnitude is 7.1 and the maximum ground acceleration is 0.3495g. Tokachi-oki (Hachinohe) Earthquake: North-south component recorded at Hachinohe City during the Tokachi-oki earthquake of May 16, 1968. The magnitude is 7.9 and the maximum ground acceleration is 0.2294g.

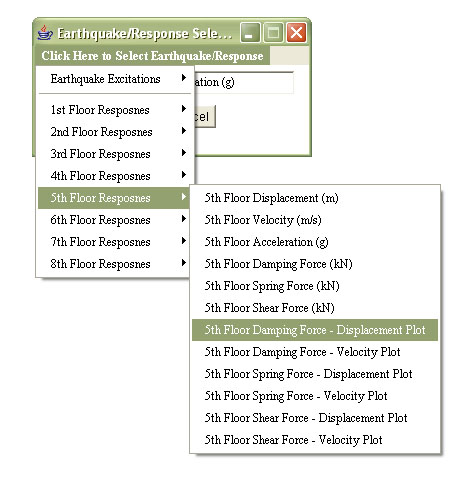Figure 4. Earthquake/Response Selection Frame

• Tokachi-oki (Hachinohe) Earthquake: North-south component recorded at Hachinohe City during the Tokachi-oki earthquake of May 16, 1968. The magnitude is 7.9 and the maximum ground acceleration is 0.2294g.

• Northridge Earthquake: North-south component recorded at Sylmar County Hospital parking lot in Sylmar, California, during the Northridge, California earthquake of Jan. 17, 1994. The magnitude is 6.8 and the maximum ground acceleration is 0.8428 g.

• Hyogo-ken Nanbu (Kobe) Earthquake: North-south component recorded at Kobe Japanese Meteorological Agency (JMA) station during the Hyogo-ken Nanbu (Kobe) earthquake of Jan. 17, 1995. The magnitude is 7.2 and the maximum ground acceleration is 0.8337g.

• N: total number of stories.

• : mass of the ith floor.

• : elastic stiffness of the ith floor.

• : damping coefficient of the ith floor.

• : ith floor displacement relative to the ground.
• : ith floor velocity relative to the ground.
• : ith floor acceleration relative to the ground.
• : ground acceleration.
• : ith floor involution coefficient for nonlinear damping model
• For the cases of hysteretic Bouc-Wen and bilinear models,
is the elastic stiffness and is the post yielding stiffness. The relationship between the yielding force and the yield displacement is

• Case I: Linear Model

The equation of motion for a single-story building (N = 1) is

The equations of motion for a multi-story building (N > 1) are

• Case II: Nonlinear Damping Model

The equation of motion for a single-story building (N = 1) is

The equations of motion for a multi-story building (N > 1) are

• Case III: Hysteretic Bouc-Wen Model

The equation of motion for a single-story building (N = 1) is

The equations of motion for a multi-story building (N > 1) are

In the above equations, the restoring force is defined as

in which is the solution of the following equation

, , , and are the shape parameters for the hysteresis loops. These parameters are defined here as

• Case IV: Hysteretic Bilinear Model

The equation of motion for a single-story building (N = 1) is

The equations of motion for a multi-story building (N > 1) are

In the above equations, the restoring force is defined as

and for i > 1

where and ; and are displacements relative to the the center of the hysteresis loop.

Figure. 6 Illustration of Displacement  and

Spring Force: force related to stiffness only.

Damping Force: force related to damping only.

Shear Force: summation of the shear and damping force.

• For an 8-story building, change the mass, stiffness and damping coefficients to achieve approximately a 1.0 Hz first natural frequency and 2% first damping ratio.

• For the default parameters, change the involution coefficient to achieve a peak reduction of maximum displacement greater than 35% under El Centro earthquake.

• For the default parameters, change the post yielding stiffness to achieve a peak reduction of displacements greater than 20% for Bouc-Wen model and great than 35% for bilinear model for both floors under El Centro earthquake

• Change the maximum amplitude of the acceleration to 1.0 (g) and then design the structure with a floor mass as 8.0 tons as nonlinear structure. Try to achieve a peak reduction of maximum displacements at least greater than 20% in all the cases under El Centro earthquake.

• Calculate the response of the structure and then evaluate the mitigation effect of the different models under different earthquake excitations.

• Newman A (1996): Special Edition Using Java. Que Cooperation, Indianapolis, IN.

  Tedesco JW, McDougal WG, Ross CA (1998): Structural Dynamics: Theory and Applications. Addison-Wesley.

  Belytschko T, Hughes TJ (1983): Computational Methods for Transient Analysis. North-Holland.

  Berg GV (1989): Elements of Structural Dynamics. Prentice Hall.

  Press WH, Flannery BP, Teukolsky SA, Vetterling WT (1987): Numerical Recipes: The Art of Scientific Computing. Cambridge University Press.