|
Table of Contents | Go to the Japanese version of this page. |
| |
| |
Welcome to the help page of the Java-Powered Simulation for Base Isolation.
Base isolation is an important strategy for protecting structures from earthquake excitations. Base isolation attempts to isolate a structure from the external ground excitations, not by trying to dissipate the energy of the earthquake within the structure, rather by not allowing this energy to even enter the structure. As a testament to this strategy, buildings in the Kansai region of Japan with base isolation devices survived the devastating 1995 Kobe Earthquake with little or no damage. This event has prompted great interest in the viability of base isolation for seismic protection of Civil structures.
This simulation considers five cases: (i) a conventional structure fixed directly to the ground; (ii) ~ (v) base isolated structures where the isolation system is installed between the structure and the ground to restrict the earthquake energy. Currently base isolation devices which are composed of rubber component and lead plug used for gaining a damping are widely applied. These components have nonlinearlities. Thus the models of base isolation system which is taken account of its nonlinearlities are newly added and the user can compare each reponse. The case (ii) is the model for the linear isolator. This isolator has both linear damping and linear stiffness. (iii) is the model for the nonlinear damping isolator. This case treats a nonlinearlty of a rubber. (iv) and (v) are the models for the hysteretic isolator. These cases deal with the nonlinearlities of lead plug which has elastic and plastic region. The characteristic of the lead plug is described by using Bouc Wen model as case (iv) and bilinear model as case (v). The structure here is modeled as a single-degree-of-freedom linear system.
The user can vary the properties of the structure, the isolation system and the earthquake motion, allowing for insight into the influence of various parameters on the responses of the system. Animation of the user designed systems facilitates visualization of parameter effects. The base isolation simulation is intended to be used to increase understanding and provide a conceptual "feel" for various parameter changes on the performance of base isolated systems.
This document offers a description of how to operate and use the Java-Powered Simulation for Base Isolation, a picture of which is shown below. In addition, technical background, including the formulation of the equations of motion and important definitions, is given, a number of "homework" problems (or exercises) are suggested, and references are provided.
![[picture of java applet]](applet.gif)
There are five components of the simulator that can be modified by the user to obtain specific and unique conditions for base isolation: (1) Control Panel; (2) Animation Frame; (3) Excitation Signal Frame; (4) Response Spectra Plot Frame; and (5) Time Response Frame. These are each identified on the above picture of the simulation page.
Located on the far right of the simulator, this panel is used to enter specific data for the structure, base isolation system and earthquake. This panel also contains the buttons to recalculate the system parameters, animate the system and perform additional functions.
Structural Parameters
- Mass: The mass of the superstructure. The default value is 100 tons.
- Natural Frequency: The natural frequency of the superstructure. The default value is 1 Hz.
- Damping Ratio: The internal damping ratio of the superstructure. The default value is 0.05.
Isolation System Parameters
- Mass Ratio: The ratio between the mass of the base slab and the mass of the superstructure (Mass Ratio = Base Floor Mass / Superstructure Mass). The default value is 0.1.
- Natural Frequency: The natural frequency of the isolated system if the superstructure is rigid. The default value is 0.5 Hz.
- Seismic Gap: The gap between the base slab and ground, as indicated below. The seismic gap should be designed to be wider than maximum base floor slab displacement to prevent collisions between the base slab and the ground. The default value for the seismic gap is 0.2 m.
Fig. 2 Diagram Showing Seismic Gap
- Damping Ratio of the Linear Isolator: The damping ratio of the the isolated system. The default value is 0.1Ns/m.
- Nonlinear Damping Involution Coefficient of the Nonlinear Damping Isolator: The nonlinear damping multiplier of the the isolated system with nonlinear damping. The default value is 0.5.
- Initial Natural Frequency of the Hysteretic Isolator: The natural frequency of the the hysteretic isolator. This value is used for elastic stiffness. The default value is 1.0 Hz. The stiffness constant after yielding (post yielding stiffness) is as same as that of linear isolator.
- Yield Displacement of the Hysteretic Isolator: The yield point of the hysteretic isolator. Over this point, the characteristic of the isolator will be changed elactic region into plastic region. The default value is 1.25 cm.
Excitation Input Parameter
- Max Amplitude: The maximum amplitude of the earthquake acceleration. The default value is the same as the original maximum acceleration of the input earthquake signal. By changing the maximum acceleration of the earthquake signal, one can compare the responses of earthquake records with different spectral contents.
- Frequency for Sine Wave: When the sinusoidal input is selected as excitation signal, It is possible to change its excitation frequency. The default value is 1.0 Hz.
Check Boxes
Check the boxes to indicate which responses you wish to display in the Time Response frame and Response Spectra Plot frame.
Response Window Zooming
Width of the excitation/response windows (in seconds) used during the animation. If your computer can't display the animation smoothly, make this number smaller.
Number of Spectra Data Point
This number shows how many ensembles into which the single time history is broken to calculate the response spectra. If you prefer short time calculation over precise drawing, make this number smaller.
Action Buttons
- Calculate: Redo the calculation according to the current input parameters. If any of the structure parameters, isolation system parameters, excitation input parameter or number of spectra data point have been changed, it is necessary to press this button. This will recalculate the responses and response spectra plots.
NOTE: Since the integration time step used for all calculations is 0.02 sec (50 Hz) the natural frequency of superstructure and the natural frequency of isolation layer should be less than 5 Hz to insure accurate results. If it takes too much time to make the calculations, it is recommended to decrease the number of spectra data points as mentioned above.
- Animate: Animate the response of the structure undergoing an earthquake excitation. Once the animation begins, the label of this button will change to the "Stop Animate" until the animation is complete. Pressing "Stop Animate" will stop the animation.
- Reset Parameters: Reset the parameters to default values.
- Results Window: This button generates (or closes) a new window to indicate system properties and calculation results.
- Help: Pressing this button will bring you to this help page.
The animation frame, located in the upper left portion of the simulation window, shows a simulation of the structural system undergoing the excitation.
Fixed Base, Linear Isolator, Nonlinear Damping, Bouc-Wen Model and Bilinear Model can be animated by the appropriate selection in the left menu of this frame.
The user can also choose to animate absolute or relative motion of the structure:
- Absolute Motion displays the response of the structure from an inertial reference frame. Thus, the ground is seen moving.
- Relative Motion displays the response of the structure from a reference frame attached to the ground.
Located in the top center of the simulation window, the earthquake signal frame shows the current earthquake signal. Four historical earthquake records are available for simulation:
- Sinusoidal Input signal: The default value of frequency is 1.0 Hz. The default value of the maximum ground acceleration is 0.3 g.
- El Centro earthquake signal: North-south component recorded at Imperial Valley Irrigation District substation in El Centro, California, during the Imperial Valley, California earthquake of May 18, 1940. The magnitude is 7.1 and the maximum ground acceleration is 0.3495g.
- Tokachi-oki (Hachinohe) earthquake signal: North-south component recorded at Hachinohe City during the Tokachi-oki earthquake of May 16, 1968. The magnitude is 7.9 and the maximum ground acceleration is 0.2294g.
- Northridge earthquake signal: North-south component recorded at Sylmar County Hospital parking lot in Sylmar, California, during the Northridge, California earthquake of Jan. 17, 1994. The magnitude is 6.8 and the maximum ground acceleration is 0.8428g.
- Hyogo-ken Nanbu (Kobe) earthquake signal: North-south component recorded at Kobe Japanese Meteorological Agency (JMA) station during the Hyogo-ken Nanbu (Kobe) earthquake of Jan. 17, 1995. The magnitude is 7.2 and the maximum ground acceleration is 0.8337g.
The user can choose to display the displacement or the acceleration signal by the proper selection of the menu.
This frame, located in the lower left of the simulation window, displays response spectra plots. The possible response spectra plots consist of displacement, velocity and acceleration.
The time response frame, located in the bottom center of the simulation window, displays the system's response due to the excitation signal shown in the Excitation Signal Frame. It can show the displacement, velocity or acceleration of the superstructure or base slab, or the shear force of the columns. Besides, not only time reponses but also displacement (or velocity) vs. restoring force (or damping force, or total force) plot can be shown in this frame. Peak response information such as maximum value of each signal, peak reduction (= maximum peak of each case / maximum peak of fixed case * 100 (%) ) or base shear is displayed in the lower portion of this frame.
(kg)
(Hz)
(kg)
(Hz)
,
damping coefficient of the superstructure
,
stiffness of the isolation layer
and damping coefficient of the isolation layer
can be calculated as following,
(N/m)
(Ns/m)
(N/m)
(Ns/m)
, post yielding stiffness 
and yielding force 
can be calculated as following,
where(N/m)
(N/m)
(N)
is the initial natural frequency of the hysteretic isolator (Hz) and 
is yield point (m).
where,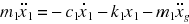
is the structural displacement relative to the ground (m).
is the structural velocity relative to the ground (m/s).
is the structural acceleration relative to the ground (m/s2).
is the ground acceleration (m/s2).
where,
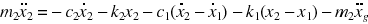
is the base floor displacement relative to the ground (m).
is the base floor velocity relative to the ground (m/s).
is the base floor acceleration relative to the ground (m/s2).
where
is nonlinear damping involution coefficient of the nonlinear damping isolator.
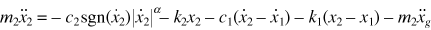
where retoring force
is
where
is the damping coefficient of hysteretic isolater and it is fixed as follows,
The default value of damping ratio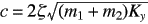
is 2%.
And 
is the solution of following equation,
, 
, 
, 
are the shape parameters for the hysteresis loops. In this case these values are fixed as
, 
, 
, 
.
To make restoring force have bilinear stiffness, it is determined according to the following rule.
Where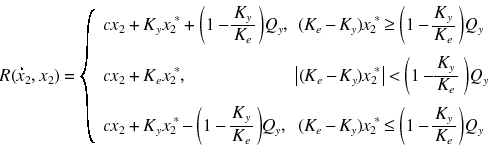
is the displacement from permanent set.
V = a / gwhere,
V : Base Shear
a : maximum acceleration of the structure (m/s2)
g : acceleration of the gravity (m/s2)
The shear force, then, is F = V W, where W is the weight of the structure.
where
or
Thus each response spectra can be written as follows: Damping Ratio
: Natural Frequency (rad/sec)
: Natural Period (sec)
: Acceleration Response Spectra
: Velocity Response Spectra
: Displacement Response Spectra
The floor response spectra uses the floor (i.e., the base slab) response acceleration instead of the input earthquake, provided that the floor motion does not change by the reciprocal action.
Kelly, James M. (1997). "Earthquake-Resistant Design with Rubber", Springer.
Structural Engineering Design Provisions. "1997 Uniform Building Code".
Teb Belytschko, Thomas J.R. Hughes. "Computational Methods for Transient Analysis", North-Holland.
Glen V. Berg. "Elements of Structural Dynamics", Prentice-Hall International.
The support of the National Science Foundation under Grant No. CMS 95-28083 (Dr. S.C. Liu, program director), and the support of the Multidisciplinary Center for Earthquake Engineering Research (MCEER) are gratefully acknowledged. In addition, we would like to thank Prof. Yozo Fujino of the University of Tokyo for his help in securing the Kobe and Hachinohe earthquake records.
